3 марта 2017
В закладки
Обсудить
Задача 20
Найдите все значения параметра \(a\), при которых уравнение \(\left| {\ln \left| x \right|} \right| = ax\) имеет три решения.
Решение
Левая часть уравнения неотрицательна. Следовательно,\(ax \ge 0\). При \(a = 0\) уравнение имеет два корня –1 и 1. Значит, \(a = 0\) не удовлетворяет условию.
Рассмотрим случай \(a > 0\). Тогда \(x \ge 0\) и поэтому \(\left| x \right| = x\). Построим график функции \(y = \left| {\ln x} \right|\). Прямая \(y = ax\) должна пересекать этот график в трёх точках. На рисунке видно, что это выполняется тогда и только тогда, когда прямая проходит внутри угла, образованного осью абсцисс и касательной \(y = {a_0}x\) к графику \(y = \ln x\) при \(x > 1\).
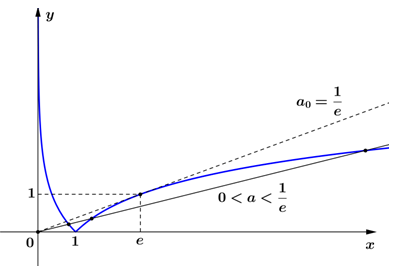
Найдем \({a_0}\). Абсцисса точки касания удовлетворяет уравнениям
\({a_0}x = \ln x,\;\;{a_0} = \frac{1}{x},\), откуда \({a_0} = \frac{1}{e},\;\;x = e\).
Таким образом, \(0 < a < \frac{1}{e}\).
Случай \(a < 0\) симметричен, то есть \( - \frac{1}{e} < a < 0\).
Ответ: \( - \frac{1}{e} < a < 0,\;\;0 < a < \frac{1}{e}\).
Решение
Левая часть уравнения неотрицательна. Следовательно,\(ax \ge 0\). При \(a = 0\) уравнение имеет два корня –1 и 1. Значит, \(a = 0\) не удовлетворяет условию.
Рассмотрим случай \(a > 0\). Тогда \(x \ge 0\) и поэтому \(\left| x \right| = x\). Построим график функции \(y = \left| {\ln x} \right|\). Прямая \(y = ax\) должна пересекать этот график в трёх точках. На рисунке видно, что это выполняется тогда и только тогда, когда прямая проходит внутри угла, образованного осью абсцисс и касательной \(y = {a_0}x\) к графику \(y = \ln x\) при \(x > 1\).

Найдем \({a_0}\). Абсцисса точки касания удовлетворяет уравнениям
\({a_0}x = \ln x,\;\;{a_0} = \frac{1}{x},\), откуда \({a_0} = \frac{1}{e},\;\;x = e\).
Таким образом, \(0 < a < \frac{1}{e}\).
Случай \(a < 0\) симметричен, то есть \( - \frac{1}{e} < a < 0\).
Ответ: \( - \frac{1}{e} < a < 0,\;\;0 < a < \frac{1}{e}\).